The Passage of Light in a Foveon Sensor

Mechanism for the Absorption of Light

The formalism for the absorption of light in the simplest case starts with a beam of light of intensity I of photons that has just penetrated into a material with a uniform concentration of absorbing material (silicon). We ignore reflection and refraction. The photons penetrate into the material and are absorbed at different depths (Fig. 0).

Figure 0. Schematic of light rays penetrating to different depths into a photon absorbing material

The mechanism for absorption is that a photon transfers all its energy to an electron in the absorbing material. The photon is "lost" from the light beam as it is absorbed in a single event. The electron is excited by the gain in energy to a higher energy state in the electron configuration around the atom. This single-event transfer of photon energy to an electron and the disappearance of the photon is closely related to the photoelectric effect where the electron is ejected from the material in a single event. The electron is ejected from the atom by the absorption of a photon. This loss of an electron leaves the atom in an excited state.

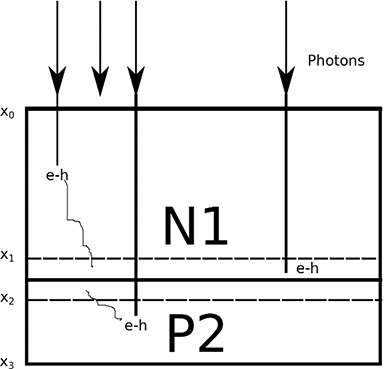
Figure 1. Schematic of light rays penetrating to different depths into a photodiode

The diode materials are "doped" which changes the absorption process a little, where the electron is ejected from the material in a single event, but the doping causes a slightly different action dependent on the type of doping. When a photon strikes an atom, an electron-hole pair e-h is created. In the N-type material x₀-x₁, the electron is held there by attraction (+ to -) and the hole drifts into the depletion region. The opposite action occurs in the P-type material x₂-x₃. In the depletion region x₁-x₂, a striking photon creates an electron-hole pair. These three actions cause an electrical charge to build up in the photodiode. To read more about the photo-electric effect, click here.

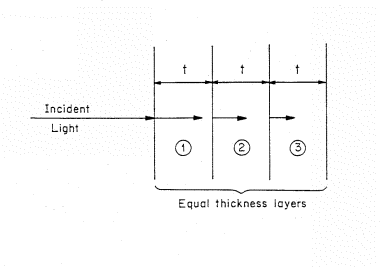
Figure 2. Light incident on a stylized Foveon sensor that is represented by a stack of equivalent thickness, t, layers. The length of the arrows decrease as the light penetrates showing the decreasing intensity of light.

The decrease in intensity of the light or photon flux as the beam penetrates into the material can be visualized if we separate the absorbing material into a set of thin, equal thickness slices of thickness t (Fig. 2). (Note: in the real Foveon sensor, the thicknesses are not equal). The material is homogeneous and a fraction of the light is absorbed in passing through a layer. The symbol I denotes the initial light intensity incident on the surface of the material. The symbol A is used to denote the fraction absorbed by each layer. Therefore, the fraction of light absorbed by each layer is A times it's incident light intensity. For example, if the fraction of light absorbed per layer is 10% (A = 0.1) of the incident flux, then for 100 photons incident on a layer, AI=0.1 x 100 i.e. 10 will be absorbed and 90 transmitted to the next layer. For three layers:

(1-A)(1-A)I=(0.9)(0.9)100=81 are transmitted.

[layer 3 - - - edit] Layer 3, (1-A)(1-A)I=81 photons incident, A(1-A)(1-A)I=0.1(0.9)(0.9)100=8 absorbed and

(1-A)(1-A)(1-A)I=(0.9)(0.9)(0.9)100=73 are transmitted.

The process ends with the remaining photons being transmitted out of the material.

The absorption of photons is given in more general form in Table 1 for an absorbed fraction A.

Table 1. Transmission for absorbed fraction A
	Incident on layer	Absorbed in layer	Transmitted through layer
layer 1	I	AI	(1-A)I
layer 2	(1-A)I	A(1-A)I	(1-A)²I
layer 3	(1-A)²I	A(1-A)²I	(1-A)³I
layer n	(1-A)^n-1I	A(1-A)^n-1I	(1-A)ⁿI

THESE EQUATIONS ARE ONLY GOOD FOR MONOCHROMATIC LIGHT BECAUSE ALPHA IS DEPENDENT ON WAVELENGTH

For 3 layers, the total absorption T_A in all layers absorbed fraction A will be

T_A=A + A(1-A) + A(1-A)² (1) The first term in equation 1 represents the absorption by the first layer. The second term represents the absorption by the second layer, and so forth.

The total transmitted light T_T though 3 layers is

T_T = (1 - A)³ (2)

Equation 1 is more conveniently written using an exponential function. Using an absorption coefficient alpha, the intensity of light at depth t, I(t) for an incident intensity I₀ is given by

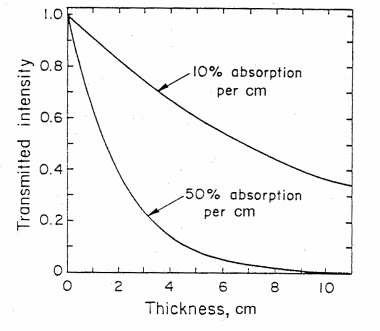
(3) where alpha is given as a fraction per distance such as 0.2 per cm. Figure 3 shows the intensity of light as a function of penetration distance into materials with two different absorption coefficients. The exponential decrease is illustrated on a linear scale by the curves in Figure 3. An increase in alpha leads to a decrease in penetration. At the depth where the product alpha t equals unity, the intensity has dropped 1/e of a factor of 0.37 times the incident intensity.

Figure 3. The intensity of light transmitted through an absorbing material as a function of thickness d in cm for (1) 10% absorbance and (2) 50% absorbance per cm. (from T. B. Brill, Light (Plenum Press, New York, 1980))

The relations rely on the fact that the fraction of light which is absorbed is independent of the intensity of the incident light. For a given wavelength of light, each successive equi-thickness of the medium aborbs an equal fraction of light passing through it, but the amount of light it receives is sucessively decreasing. Hence, the intensity of light passing though a medium will decrease with depth. [HORRIBLE] This is an exponential relation, derived from:
The number of delta-I of photons which are absorbed in a given thickness delta-x is proportional to the incident intensity I or the number I incident on it:

(4) If we use the symbol alpha to denote the absorption coefficient where alpha is the fraction of photons absorbed per unit thickness, then Eqn. 4 can be written:

(5) or in standard differential notation as:

(6) This equation can be integrated from the surface at X=0 to a depth x, and leads to the relation that the intensity I(x) at depth x is given by

(7) where I₀ is the number of photons at x=0, I₀=I(x=0).

The absorption coefficient is a number per unit distance, such as 0.1 per cm which can be written 0.1 cm^-1. At a depth x where alpha x equals unity (in this example, x=10 cm as 0.1 x 10 =1) the number of photons decreases by a factor of 1/e or 0.37 (the value of e=2.718).

For small values of alpha x, for example alpha x =0.01, Eqn 7 can be written as a linear expansion:

(8) This ties into the presentation of the format in Table 1.

more blah relative to Foveon unequal depths needed + actual image rot 90 left